演算法的簡單定義:輸入 + 演算法 = 輸出
這一篇文章有非常詳細的介紹演算法是什麼:初學者學演算法-談什麼是演算法和時間複雜度
一般判斷演算法的好壞是使用『空間複雜度』和『時間複雜度』來評估,
所謂時間複雜度,指的是執行一段演算法,跑完整個運算邏輯所要花的時間。
雖然這個複雜度名為『時間複雜度』,但實際上,我們要真正衡量某個演算法時,是以步驟次數來看。
如果一個演算法執行的步驟是固定的,無關輸入的值而改變,那我們會記成 O(1),例如:
function(int n){
print(n);
}
而下面這個演算法:
function(int n){
for(i=0;i<n;i++){
for(j=0;j<n-1;j++){
print(i*j);
}
}
}
這個演算法則是依據輸入的 n 的數量會跑 n 次,所以是 O(n)。
有時若跑的次數較不固定,如:
function(int n){
for(i=0;i<n;i++){
for(j=0;j<n-1;j++){
print(i*j);
}
}
}
這個演算法雖然跑了 n×(n−1)=n2−n 次,但我們還是會記做 O(n2) ,也就是說,只要找出最高次方,並且把係數拿掉即可。
而一個程式的空間複雜度是指完全地執行程式所需的記憶體量。
例如下面這個函式,不管程式跑了幾遍,都不會影響使用的變數數量:
function(int n){
for(int i=0;i<n;i++){
print(i);
}
}
故該函式的空間複雜度記做 O(1)。
但下面這個函式,會隨著丟進去的數字而影響變數的量,例如:
function(int n){
int c[n];
for(int i=0;i<n;i++){
c[i] = i;
}
}
故該函式空間複雜度為 O(n)。
遞迴的空間複雜度一般是與最深的呼叫深度成正比,若遞迴中有局部的變數或參數,所需的空間複雜度會更高。
人工智慧也是演算法的一種,如著名的旅行推銷員問題(Travelling salesman problem, TSP),在假定已知每個城市間的距離,在不重複訪問同一個城市下,如何求出最快速的行程組合,這就已經是電腦科學中著名的難解問題。
(Source:By Saurabh.harsh)
一筆畫問題也是很經典的演算法議題。一筆畫問題是柯尼斯堡七橋問題經抽象化後的推廣,是圖遍歷問題的一種。在柯尼斯堡問題中,如果將橋所連接的地區視為點,將每座橋視為一條邊,那麼問題將變成:對於一個有著四個頂點和七條邊的連通圖G(S,E),能否找到一個恰好包含了所有的邊,並且沒有重複的路徑。歐拉將這個問題推廣為:對於一個給定的圖,怎樣判斷是否存在著一個恰好包含了所有的邊,並且沒有重複的路徑?這就是一筆畫問題。

(Source:By 維基百科)
這個問題的解答是:如果一個圖能一筆畫成,那麼對每一個頂點,要麼路徑中「進入」這個點的邊數等於「離開」這個點的邊數:這時點的度為偶數。要麼兩者相差一:這時這個點必然是起點或終點之一。注意到有起點就必然有終點,因此奇頂點的數目要麼是0,要麼是2。
在程式之美-微軟技術面試心得裡,也給了讀者了許多很經典的演算法題目,例如:構造數獨遊戲、一疊蔥油餅的排序、一排石頭的遊戲、俄羅斯方塊遊戲、踩地雷遊戲的機率、連連看遊戲,都是我感到十分有興趣的演算法議題。
後來因為我小時候很喜歡玩kawai連連看,所以就選擇這款遊戲做為這次鐵人賽的題目,書中對於連連看遊戲所給的思考方向如下:
假如讓你來設計一個連連看遊戲的演算法,你會怎麼做呢?要求如下:
- 如何用簡單的電腦模型來描述這個問題?
- 如何判斷兩個圖形能否相消?
- 如何求出兩個相同圖形間的最短路徑?(轉彎數最少、路徑經過的格子數目最少)
- 如何確定目前是處於僵局狀態,並設計演算法來解除僵局?
在經典的最短路徑當中,需要求出經過格子數目最小的路徑。這邊為了確保轉彎次數最少,需要把最短路徑問題的目標函數修改為從一個點到另一個點。雖然目標函數修改了,但演算法的框架仍然可以保持不變。廣度優先搜尋是解決經典最短路徑問題的一個思考方向。
根據上面的說明,我們若想要做一個連連看的遊戲,需要思考解決下列問題:
因此,我們至少會需要使用到圖形(Graph)演算法以及搜尋(包含深度與廣度搜尋)演算法。
下面我們便先針對這兩個部份的演算法來做介紹。
一張圖由數個點( vertex )以及數條邊( edge )所構成。點與點之間,得以邊相連接,表示這兩點有關聯、關係。
那要如何利用程式語言來表示一張圖?有下列幾種方法(資料來源於此):
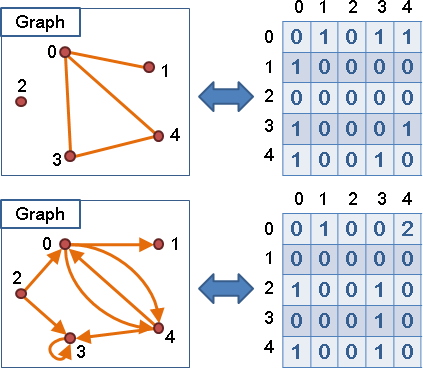
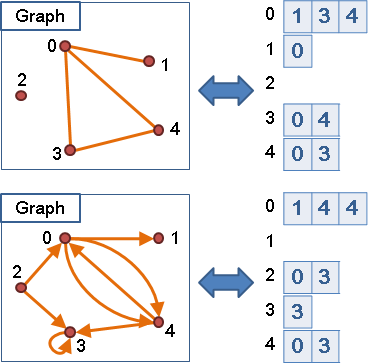
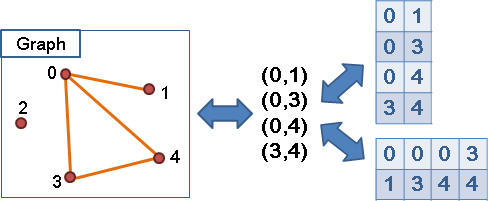
圖的遍歷,也就是指通盤地讀取圖的資訊:決定好從哪裡開始讀,依照什麼順序讀,要讀到哪裡為止。詳細地設計好流程,始能通盤地讀取圖的資訊;如果設計得漂亮,在解決圖的問題時,還可以一邊讀取圖的資訊,一邊順手解決問題呢!利用最簡單的資料結構 queue 和 stack ,就能製造不同的遍歷順序,得到兩種遍歷演算法: Breadth-first Search(廣度優先搜尋) 和 Depth-first Search (深度優先搜尋)。
下面是這篇文章裡對深度優先搜尋法所給的解釋:
深度優先搜尋法,是一種用來遍尋一個樹(tree)或圖(graph)的演算法。由樹的根(或圖的某一點當成 根)來開始探尋,先探尋邊(edge)上未搜尋的一節點(vertex or node),並儘可能深的搜索,直到該節點的所有邊上節點都已探尋;就回溯(backtracking)到前一個節點,重覆探尋未搜尋的節點,直到找到目 的節點或遍尋全部節點。
深度優先搜尋法屬於盲目搜索(uninformed search)是利用堆疊(Stack)來處理,通常以遞迴的方式呈現。
範例: 以深度優先搜尋法找出下圖的所有節點順序:
假設起始點為 A,且每一節點由左至右的順序來搜尋下個節點,則結果為: A, B, E, F, D, C, G
下面是這篇文章裡對廣度優先搜尋法所給的解釋:
廣度優先搜尋法,是一種圖形(graph)搜索演算法。從圖的某一節點(vertex, node)開始走訪,接著走訪此一節點所有相鄰且未拜訪過的節點,由走訪過的節點繼續進行先廣後深的搜尋。以樹(tree)來說即把同一深度(level)的節點走訪完,再繼續向下一個深度搜尋,直到找到目的節點或遍尋全部節點。
廣度優先搜尋法屬於盲目搜索(uninformed search)是利用佇列(Queue)來處理,通常以迴圈的方式呈現。
範例: 廣度優先搜尋法找出下圖的所有節點順序:
假設起始點為 A,且每一節點由左至右的順序來搜尋下個節點,則結果為: A, B, C, D, E, F, G
以連連看來說,因為在連連看的棋盤裡,任意兩個同一排或同一列的點,都可以做直線相連,我們若用一個二維陣列直接來儲存棋盤內容,可以用該陣列第一個索引值或第二個索引值是否相同,來判別是否在同一條線上。
若圖形為10X10的棋盤,則陣列設計如下:
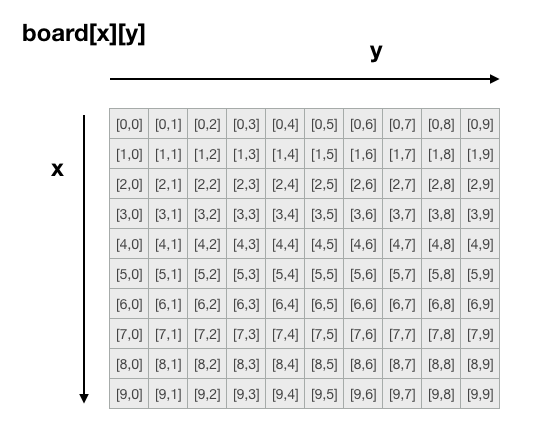
用這樣的陣列的儲存方式,我們可以注意到,上圖的x,y軸的位置,和一般我們在做遊戲時的x,y軸的方向會剛好相反,這一點要特別注意,才不會在計算點與點間的位置時出錯。
而路徑的部份則使用上面圖演算法中的關連矩陣去紀錄,如[[0,0],[-1,0],[-1,8],[0,8]],在連連看遊戲裡,每一個合法的路徑都應由四個或以內的點所組成成。並且每一個點之間,必定要有相同的x或相同的y。我們可以用這樣的條件去搜尋判斷可能存在的路徑。
在一般我們做最短路徑搜尋的情況,都會以廣度優先搜尋為主。
在連連看裡面,連線的線條不可大於兩個轉彎處,兩個轉彎處的意思,代表連接的線最多只能由三條直線來組成。
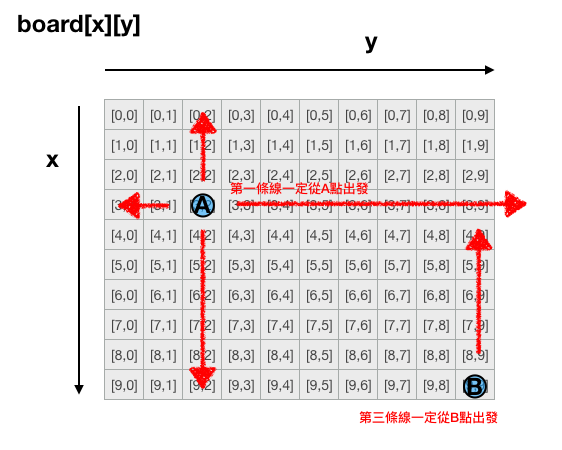
由上圖可以發現,我們可以以直線做為搜尋單元,先搜尋A點上、下、左、右最遠能到達的點,對比B點上、下、左、右最遠可以到達的點,判斷是否有可能可以形成一條連線,若有可能,再去尋找是否中間存在可能的第二條線。
